Rotations on the Coordinate Plane

This is proportionality rather than an equation because Maxwell’s equations only specify the direction of E—we are free to choose the amplitude. Because Fresnel’s equation gives two values for n, (5.59) specifies two distinct polarization components associated with each propagation direction uˆ . These polarization components form a natural basis for describing light propagation in a crystal. When light is composed of a mixture of these two polarizations, the two polarization components experience different indices of refraction.
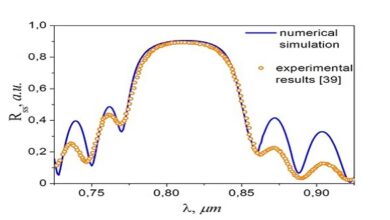
We can use (5.59) to study the behavior of polarization direction as the direction of propagation varies. plots of the polarization direction (i.e. normalized Ex , Ey , and Ez ) in Potassium Niobate as the propagation direction is varied. The plot is created by inserting the spherical representation of uˆ (5.24) into Fresnel’s equation (5.20) for a chosen sign of the ±, and then inserting the resalting n into (5.59) to find the associated electric field.
As we saw in Example 5.4, at θ = 0 the light associated with the slow index is polarized along the y-axis and the light associated with the fast index is polarized along the x-axis. we have plotted the angle between the two polarization components. At θ = 0, the two polarization components are 90◦ apart, as you might expect. However, notice that in other propagation directions the two linear polarisation components are not precisely perpendicular. Even so, the two polarization components of E are orthogonal in a mathematical sense,6 so that they still comprise a useful basis for decomposing the light field.
Discover the essence of crafting captivating magazine content, delving into the art of storytelling and visual aesthetics. Uncover the secrets to engaging readers through compelling narratives and striking imagery, elevating the impact of each page turn. Master the intricacies of magazine creation to resonate with diverse audiences and leave a lasting impression.
Determining the Fields in a Uniaxial Crystal.
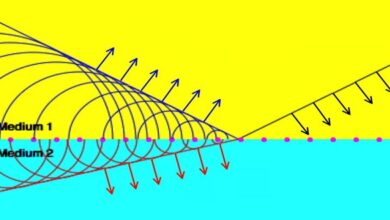
In 1690 Christian Huygens developed a way to predict the direction of extraordinary rays in a crystal by examining an elliptical wavelet. The point on the elliptical wavelet that propagates along the optic axis is assumed to experience the index ne. The point on the elliptical wavelet that propagates perpendicular to the optic axis is assumed to experience index no.
It turns out that Huygens’ approach agreed with the direction of energy propagation (5.40) (as opposed to the direction of the k-vector). This was quite satisfactory in Huygens’ day (except that he was largely ignored for a century, owing to Newton’s corpuscular theory) since the direction of energy propagation is what an observer sees.
When the direction of the electric field of light oscillates in a regular, predictable fashion, we say that the light is polarized. Polarization describes the direction of the oscillating electric field, a distinct concept from dipoles per volume in a material P – also called polarization. In this chapter, we develop a formalism for describing polarized light and the effect of devices that modify polarization. If the electric field oscillates in a plane, we say that it is linearly polarized.
The electric field can also spiral around while a plane wave propagates, and this is called circular or elliptical polarization. There is a convenient way for keeping track of polarization using a two-dimensional Jones vector. Figure 6.1 Animation showing different polarization states of light. Many devices can affect polarization such as polarizers and wave plates.
Last word
Their effects on a light field can be represented by 2×2 Jones matrices that operate on the Jones vector representing the light. A Jones matrix can describe, for example, a polarizer oriented at an arbitrary angle or it can characterize the influence of a wave plate, which is a device that introduces a relative phase between two components of the electric field.